توزیع نرمال (Normal Distribution) یا توزیع گوسی (Gaussian Distribution)

مدرس: مسعود کاویانی

MasoudKaviani.ir

در درس قبلی با مقدماتی در مورد احتمالات و توابع توزیع شده آشنا شدید. در این درس به یکی از توزیع‌های معروف به اسم توزیع نرمال می‌رسیم و کاربردهای مختلفِ آن را با یکدیگر مرور می‌کنیم. توزیع نرمال یا همان توزیع گوسی، در بسیاری از داده‌ها، مشاهده می‌شود. در واقع بسیاری از فرآیند‌های این جهان، داده‌هایی بر اساس توزیع نرمال دارند.

فرض کنید یک فلافل فروشیِ بزرگ دارید. هر روز تعدادی مشتری به این مغازه‌ی شما وارد می‌شوند و از شما خرید می‌کنند. شما این تعداد را در طی ۱۰۰ روز شمارش کرده و به نموداری مانند تصویر زیر می‌رسید:

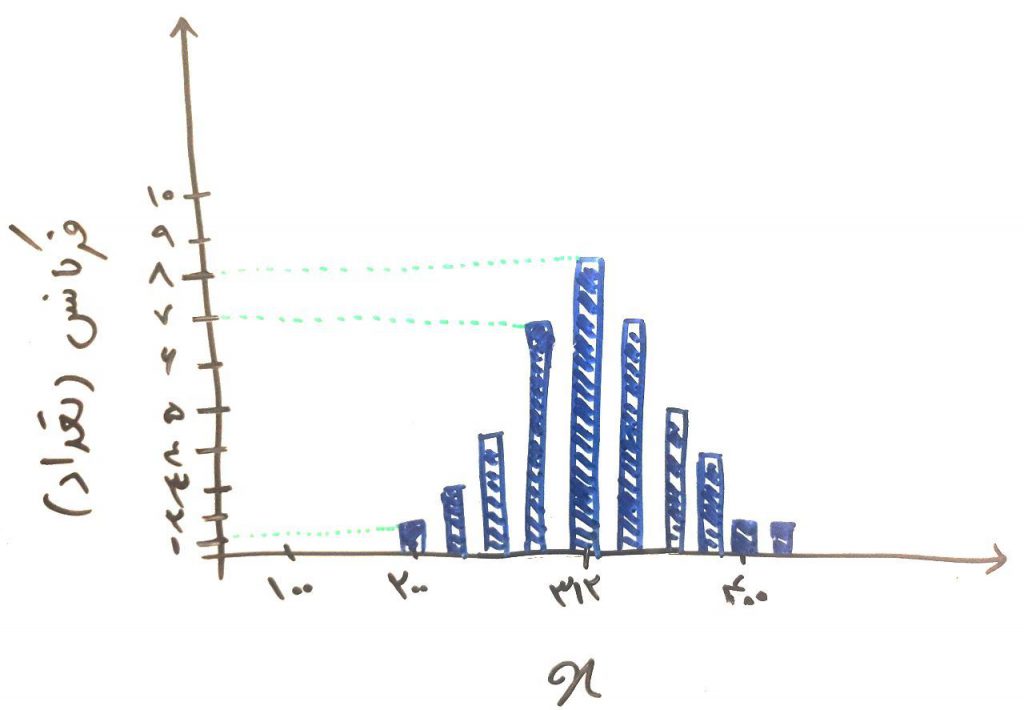
محور افقی تعداد مشتریان را نشان می‌دهد و محور عمودی، تعداد تکرار را. برای مثال در ۸ روز از این ۱۰۰ روز، شما تعداد ۳۱۲ مشتری داشته‌اید و یا فقط یک روز بوده که تعداد مشتریان شما ۴۰۰ عدد شده است. به نمودار بالا، نمودار هیستوگرام (histogram) نیز می‌گویند. فرض کنید به طور میانگین تعداد مشتریان شما در روز ۳۱۳ عدد هستند. البته این تعداد متغیر است. پس انحراف استاندارد را برای این مشتریان نیز محاسبه می‌کنیم که بر فرض مثال، برابر ۵۷ نفر می‌شوند. اگر درسِ انحراف استاندارد را خوانده باشید، متوجه می‌شوید که منظورمان این است که داده‌ها در محدوده‌ی ۳۱۳ تجمع کرده و به طور میانگین ۵۷ عدد بالاتر یا ۵۷ عدد پایین‌تر پراکنده شده‌اند. برای فهم بهتر شکل زیر را نگاه کنید:

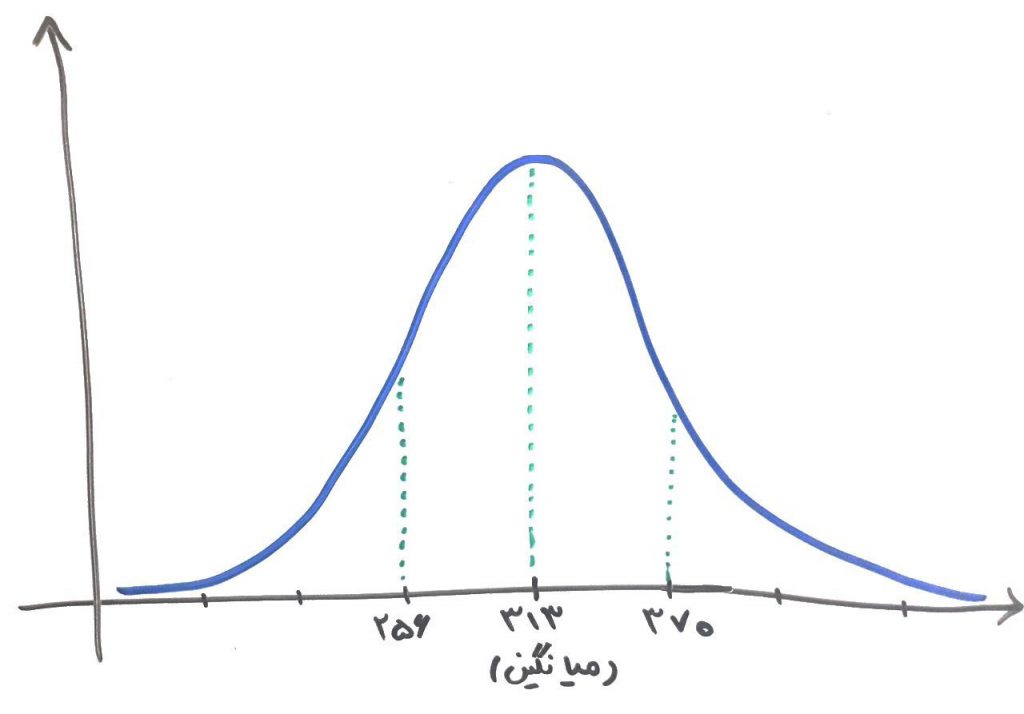
همان‌طور که می‌بینید، بیشتر داده‌ها در میانگین، یعنی همان ۳۱۳ قرار دارند و هر چقدر از ۳۱۳ فاصله می‌گیریم، احتمال وقوعِ آن داده‌ها کمتر می‌شود. اگر نمودار مانند شکل بالا زنگوله‌ای باشد، به آن نمودار توزیع گوسی یا نمودار توزیع نرمال می‌گویند. در توزیع نرمال به صورت تجربی اثبات شده است که ۶۸ درصد از داده‌ها در فاصله‌ی ۱ برابریِ انحراف استاندارد از میانگین قرار دارند. در مثال بالا، یعنی ۶۸ درصد داده‌های ما در بازه‌ی ۲۵۶ (۵۷ – ۳۱۳) تا ۳۷۰ (۵۷ + ۳۱۳) قرار می‌گیرند. به این معنی که در آن ۱۰۰ روزی که ما مشتریانِ مغازه‌ی فلافل فروشی را مورد ارزیابی قرار دادیم، ۶۸ روز از آن ۱۰۰ روز، تعداد مشتریان بین ۲۵۶ تا ۳۷۰ بوده است. در توزیع نرمال همچنین به صورت تجربی اثبات شده است که ۹۵ درصد داده‌ها در فاصله‌ی ۲ برابریِ انحراف استاندارد، نسبت به میانگین قرار داشته و ۹۹.۷ درصد از داده‌ها در فاصله‌ی ۳ برابریِ انحراف استاندارد نسبت به میانگین، قرار گرفته‌اند.

شکل بالا در واقع نوعی تابع توزیع احتمالی (PDF) بود که در درس قبل به آن پرداختیم. اگر داده‌های ما توزیع نرمال داشته باشند، تابع توزیع احتمال را می‌توان با استفاده از فرمول زیر محاسبه کرد:

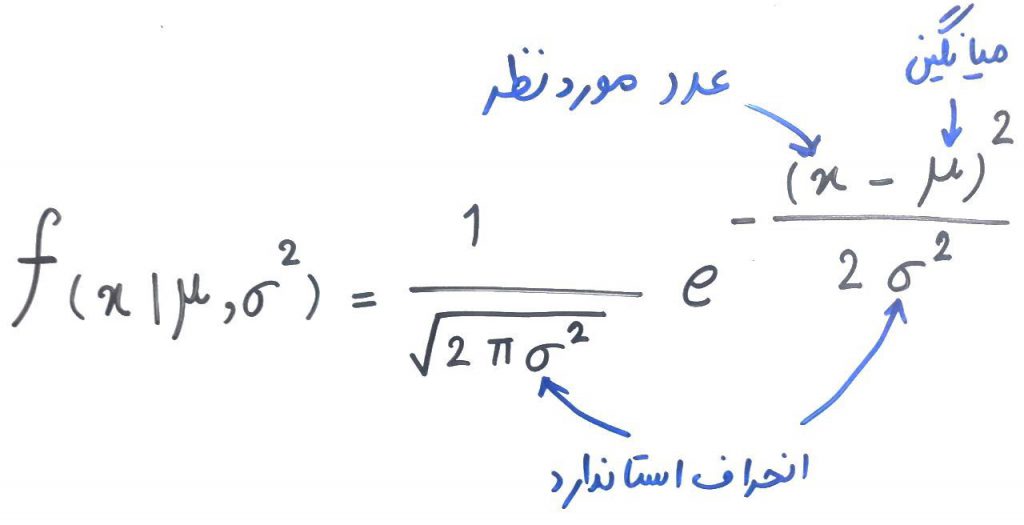
همان‌طور که می‌بینید در این فرمول، بایستی میانگین و انحراف استاندارد را داشته باشیم که این اعداد از روی داده‌هایی که جمع‌آوری کرده‌ایم به دست می‌آیند. برای حل یک مسئله مقداری که می‌خواهیم احتمال کمتر از آن را به دست بیاوریم، به جای متغیرِ x می‌گذاریم، و این فرمول به ما آن احتمال را خواهد داد. برای مثال در مسئله‌ی فلافل فروشی، می‌خواهیم بدانیم که در یک روز، با چه احتمالی تعداد مشتریانِ ما حدودا ۳۰۰ می‌شود؟ برای پاسخ به این سوال باید مقدار میانگین (۳۱۳)، انحراف استاندارد (۵۷) و x که همان ۳۰۰ هست را در فرمول بالا بگذاریم.

همچنین ما تابع توزیع تجمعی (CDF) را داشتیم که توسط آن می‌توانستیم بگوییم که با چه احتمالی یک نمونه کمتر از یک مقدار خاص می‌شود. برای مثال اگر بخواهیم بدانیم که در یک روز در فلافل فروشی ما، با چه احتمالی، تعداد ۳۰۰ نفر یا کمتر مشتری داریم باید از تابع توزیع تجمعی یا همان CDF استفاده کنیم. چیزی مانند شکل زیر:

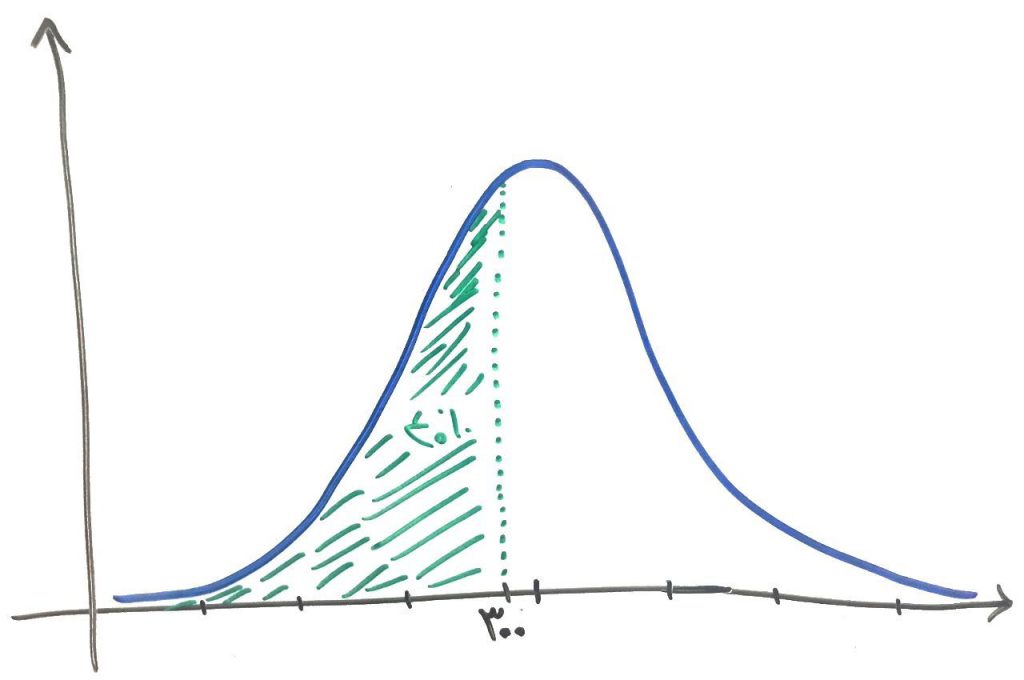
حالا فرض کنید فلافل فروشی می‌خواهد بداند با چه احتمالی، در یک روز بیشتر از ۴۰۰ مشتری خواهد داشت. برای این کار بایستی ابتدا احتمالِ کمتر از ۴۰۰ مشتری را حساب کرده و بعد این احتمال را از ۱ کم کنیم. مثلاً اگر احتمال حضورِ مشتری کمتر از ۴۰۰ عدد در یک روز برابر ۰.۹۴ شد (یعنی ۹۴ درصد)، پس احتمال حضورِ بیش از ۴۰۰ مشتری برابر ۶ درصد (۰.۹۴ – ۱ ) خواهد شد. پس این‌جا ساندویچ فروش می‌تواند تصمیم بگیرد که منابع خود را برای ۴۰۰ مشتری آماده کند و قبول کند که در ۶ درصد از مواقع ممکن است ساندویچ کم بیاورد.

همچنین می‌توان با بازی کردن با فرمولِ توزیع نرمال به سوال‌هایی مانند این پاسخ داد که مثلاً چند عدد ساندویچ در روز آماده کنیم تا در ۹۸ درصد از مواقع، ساندویچ کم نیاوریم. در واقع در فرمولِ بالا، می‌خواهیم این بار x را محاسبه کنیم.

مثال جالب دیگری که می‌توان از کاربردهای توزیع نرمال بیاوریم، مسئله‌ی مسیریابی است. فرض کنید در یک نرم‌افزارِ مسیریابی برای رفتن از نقطه‌ی A به نقطه‌ی B، دو مسیر وجود دارد. داده‌ها به ما گفته‌اند که از توزیع نرمال پیروی می‌کنند. با توجه به داده‌های قبلی متوجه شده‌ایم که مسیر اول به صورت میانگین ۵۴ دقیقه با انحراف استاندارد ۳ دقیقه زمان‌بر است. مسیر دوم نیز ۶۰ دقیقه زمان برده ولی انحراف استاندارد ۱۰ دقیقه‌ای دارد. مسئله این است که برای رفتن از نقطه‌ی A به نقطه‌ی B، اگر فقط ۵۰ دقیقه وقت داشته باشیم، بهتر است کدام مسیر را انتخاب کنیم؟ با استفاده از فرمولِ PDF برای توزیع نرمال به داده‌های زیر می‌رسیم:

۱: Prob(Time < 50) = 0.0912
2: Prob(Time < 50) = 0.1586

همان‌طور که مشاهده می‌کنید، اگر بخواهیم در کمتر از ۵۰ دقیقه به مقصد برسیم، مسیر دوم، به نظر بهتر است، چون احتمال بالاتری برای عدد ۵۰ به ما می‌دهد.

همان‌طور که فهمیدید، توزیع نرمال یا همان normal distribution، در مسائل مختلف و متفاوتی کاربرد دارد. البته این‌که بخواهیم بفهمیم داده‌های ما از توزیع نرمال پیروی می‌کنند نیز خود یک چالش است. می‌توانیم توسط ابزارهای مختلف، هیستوگرام برای داده‌ها را بر روی محور مختصات رسم کرده و اگر نمودار زنگوله‌ای را مشاهده کردیم، بفهمیم که توزیع نرمال داریم و آن وقت است که می‌توانیم از فرمول‌های توزیع نرمال استفاده کنیم. البته روش‌های محاسباتی نیز برای ارزیابیِ داده‌ها وجود دارند تا توسط آن بتوانیم بفهمیم که آیا داده‌های ما به صورت نرمال توزیع شده‌اند یا خیر.